中考数学最怕几何题?让这份最全几何解题模型来帮你!
【千问解读】
全等变换
平移:平行等线段(平行四边形)
对称:角平分线或垂直或半角
旋转:相邻等线段绕公共顶点旋转
对称全等模型:
说明:
以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型

说明:
上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型
半角:有一个角含1/2角及相邻线段
自旋转:有一对相邻等线段,需要构造旋转全等
共旋转:有两对相邻等线段,直接寻找旋转全等
中点旋转:倍长中点相关线段转换成旋转全等问题
旋转半角模型
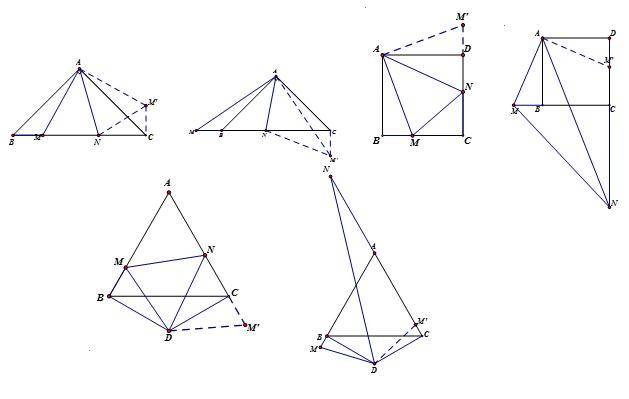
说明:
旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型
构造方法:
遇60度旋60度,造等边三角形
遇90度旋90度,造等腰直角
遇等腰旋顶点,造旋转全等
遇中点旋180度,造中心对称
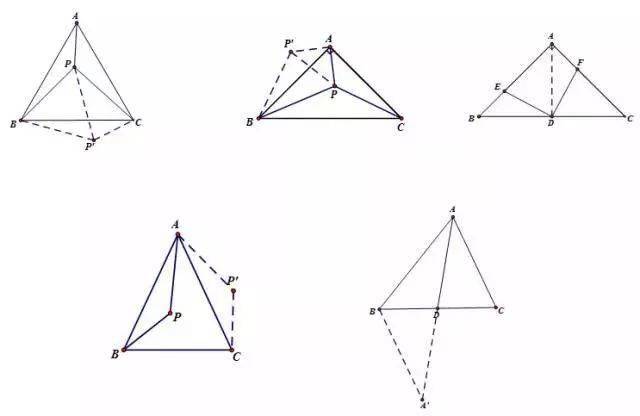
共旋转模型

说明:
旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形
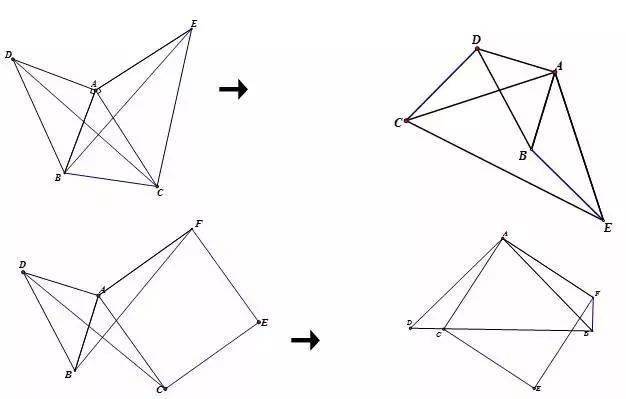
说明:
模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
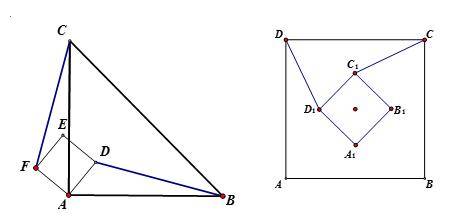
中点旋转:

说明:
两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型
对称最值(两点间线段最短)
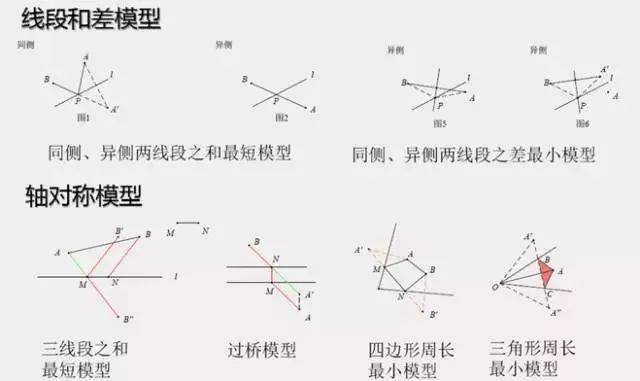
对称最值
(点到直线垂线段最短)
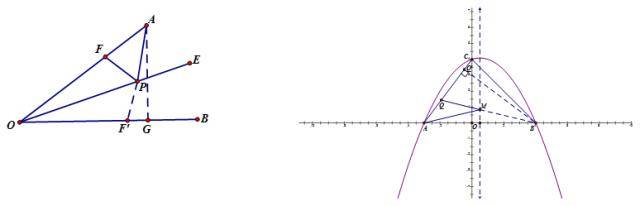
说明:
通过对称进行等量代换,转换成两点间距离及点到直线距离。
旋转最值
(共线有最值)
说明:
找到与所要求最值相关成三角形的两个定长线段,定长线段的和为最大值,定长线段的差为最小值。
简拼模型
三角形→四边形
四边形→四边形
说明:
剪拼主要是通过中点的180度旋转及平移改变图形的形状。
矩形→正方形
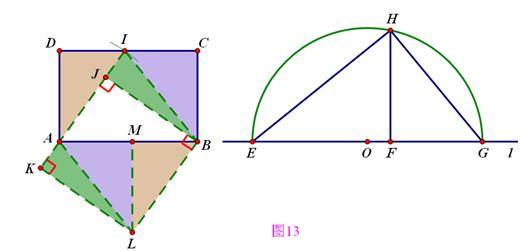
说明:
通过射影定理找到正方形的边长,通过平移与旋转完成形状改变
正方形+等腰直角三角形→正方形

面积等分
旋转相似模型
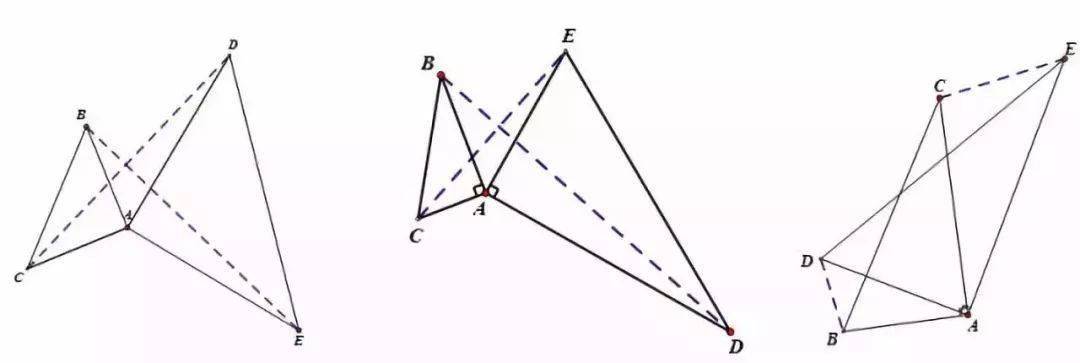
说明:
两个等腰直角三角形成旋转全等,两个有一个角是300角的直角三角形成旋转相似。
推广:两个任意相似三角形旋转成一定角度,成旋转相似。
第三边所成夹角符合旋转“8”字的规律。

相似模型
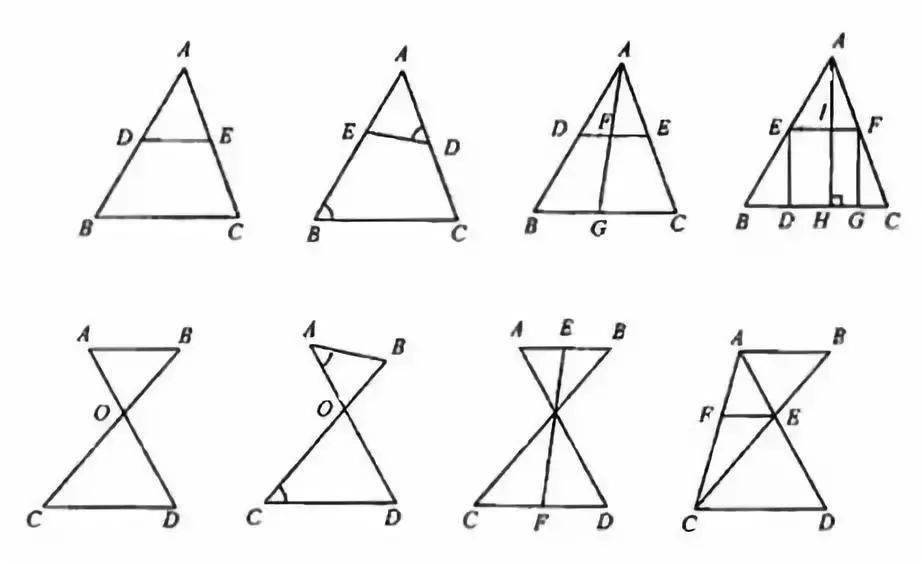
说明:
注意边和角的对应,相等线段或者相等比值在证明相似中起到通过等量代换来构造相似三角形的作用。

说明:
(1)三垂直到一线三等角的演变,三等角以30度、45度、60度形式出现的居多。
(2)内外角平分线定理到射影定理的演变,注意之间的相同与不同之处。
另外,相似、射影定理、相交弦定理(可以推广到圆幂定理)之间的比值可以转换成乘积,通过等线段、等比值、等乘积进行代换,进行证明得到需要的结论。
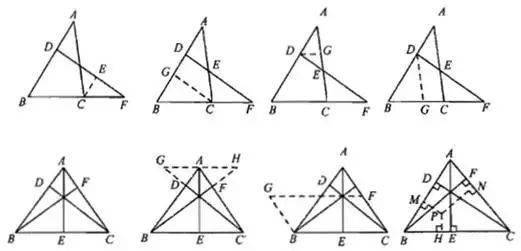
说明:
相似证明中最常用的辅助线是做平行,根据题目的条件或者结论的比值来做相应的平行线。


中点模型
【模型1】倍长
1、 倍长中线;2、倍长类中线;3、中点遇平行延长相交
【模型2】遇多个中点,构造中位线
1、 直接连接中点;2、连对角线取中点再相连
【例】在菱形ABCD和正三角形BEF中,∠ABC=60°,G是DF的中点,连接GC、GE.
(1)如图1,当点E在BC边上时,若AB=10,BF=4,求GE的长;
(2)如图2,当点F在AB的延长线上时,线段GC、GE有怎样的数量和位置关系,写出你的猜想;并给予证明;
(3)如图3,当点F在CB的延长线上时,(2)问中关系还成立吗?写出你的猜想,并给予证明.
角平分线模型
【模型1】构造轴对称
【模型2】角平分线遇平行构造等腰三角形
【例】如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,交AD边于H,延长BA到点G,使AG=CF,连接GF.若BC=7,DF=3,EH=3AE,则GF的长为
手拉手模型
邻边相等的对角互补模型
【例】如图,矩形ABCD中,AB=6,AD=5,G为CD中点,DE=DG,FG⊥BE于F,则DF 为
半角模型
弦图模型
最短路径模型
【两点之间线段最短】
1、将军饮马
2、费马点
【垂线段最短】
【两边之差小于第三边】
责任编辑:
千叟宴当作清朝盛世的顶点 该盛宴为什么也是清朝衰落的开始
1796年,是做了60年皇帝之后,禅位给帝的第一年。
为了庆祝乾隆皇帝60年来的“文治武功”和嘉庆帝登基,这年正月初五,在宁寿宫和皇极殿大摆筵席,举行“千叟宴”5900多名年60岁以上的老人,欢聚一堂,举杯祝酒,场面隆重热烈。
这样的“千叟宴”1785年一月在“乾清宫”也举行过一次,10年以后的今天,再次举行,意义更加重大。
“千叟宴”的酒席摆了五六百桌,偌大的皇极殿和宁寿宫,席面上金杯玉碟,山珍海味,名酒佳肴一应俱全。
在5900名应邀参加宴会的老人中年逾百岁的有十几位,他们受到特别尊敬,入御席与乾隆皇帝共宴,皇帝赐酒赐诗,人人兴高釆烈,齐声同呼“太上皇”!这一年,乾隆皇帝虽然也是85岁高龄的老人了,但他还是,,亲自到席间去祝酒助兴。
数千名白发苍苍的老人,同饮殿庭,共颂皇恩,可以说是乾隆盛世的一个缩影。
乾隆皇帝,名叫弘历,1735年雍正帝逝世,24岁的弘历即位,第二年为乾隆元年到1796年,他已经做了整整60年的皇帝,为了不超过他祖父帝在位61年的记录,便禅位给他的十五子,自己称太上皇。
“千叟宴”就是乾隆帝禅位,嘉庆帝即位的盛大庆典。
乾隆皇帝统治的半个多世纪里,“文治武功”,盛极一世,清王朝的发展到了最高峰。
在社会经济方面,乾隆年间达到了建国以来的最高峰。
全国人口超过2亿,耕地面积达到741万余顷,兴修水利也取得了很大的成绩。
在政治方面,得到空前的发展,多民族国家有了进一步的巩固。
乾隆年间,的版图,北至恰克图,南至海南岛、团沙群岛,西至葱岭,东到外兴安岭、库页岛。
全国内地18省以外,还有直属中央的顺天府和东北的盛京地区。
新疆西藏,内、外蒙古等边境藩部,也都是清朝管辖范围,四周还有一些依附的属国。
大清帝国已经成为一个幅员广阔,国势强大的统一封建国家,赫然屹立在东方大地。
在“文治”方面,最著名的是编辑《四库全书》。
乾隆三十七年(1772),成立了《四库全书》馆,以为总裁官,花了10年左右的时间,才告完成。
《四库全书》共收书361种,79009万卷。
每当一部书籍校订完成,就由馆臣拟写一篇提要放在书前。
分为经、史、子、集四类,装订成36万余册。
《四库全书》是我国最大的一部丛书,保存了许多珍贵的文献资料,它是我国极其宝贵的文化遗产,具有很高的史料价值。
但是乾隆皇帝也借编辑《四库全书》之机,对全国所存的书籍作了一番大检查,其中不少的书籍被列为禁书,没能编入《全书》,有的书籍虽编入《全书》,但部分内容被删节。
在编书的几年里,全国销毁禁书三千余种,六七万卷以上,古籍文献遭到了一次大浩劫,不少书籍失传。
乾隆、嘉庆之际,一方面由于大兴,一部分学者心有余悸;另一方面由于编纂《四库全书》的需要,考订和整理古籍得到清统治者的提倡和鼓励,因而许多人埋头于古典文献的考订,出现了考据学热潮,史称“乾嘉考据学”,或称“乾嘉学派”。
考据学从校订经书开始,后来扩大到史籍和;从解释经义,扩大到考究历史、地理、文字音韵、天文历法、典章制度等各个领域。
虽然有它消极的一面,但也在一定范围内繁荣了清朝的文化。
在“武功”方面,乾隆一代有所谓“十全武功”之说,乾隆皇帝晚年也自称“十全老人”。
所谓“十全”,是指10次较大规模的战争,有些是平定边境地区的叛乱,有些是镇压各族人民的反抗。
“十全武功”必不可免地要加重人民的负担,破坏社会的生产,但其中对边境少数分裂叛乱分子的镇压,又是有进步意义的。
它使清朝对边境地区的统治得到了加强,进一步巩固了清朝的疆域。
康熙盛世,陶醉在盛世之中,,生活极端腐化。
乾隆皇帝在位60年,几乎三年两头都要外出巡游。
巡游虽然也有加强对各地控制的目的,但主要的是为了满足他个人腐化享乐的欲望。
他南到江浙,西到五台山东到山东辽宁,北到塞外蒙古。
其中江南地区巡了6次,因此留下了许多“乾隆皇帝游江南”的传说。
他每次下江南,地方官都要及早准备,河里龙舟彩栅,千里不断。
乾隆皇帝要上岸的地方还要上搭篷帐,下铺锦毯,修行宫,盖别墅,采办精美家具。
搜寻奇花异石。
准备名菜美肴供皇帝及随从官员品尝。
这笔巨大的开支都不在国家财政开支之列。
统统向地方科派。
极大地加重了各地人民的负担。
乾隆皇帝的母亲做寿。
在西华门至西直门外十几里长的路上搭建的各种楼阁。
都由各省进献。
各省总督巡抚为了讨好皇帝。
便挖空心思。
争艳夺美。
实际上是一次奢侈华丽的楼阁展览与竞赛。
如广东的“翡翠亭”,二三丈宽,全用孔雀尾部羽毛做屋瓦,一只亭子,不知用了多少只孔雀羽毛;湖北的“黄鹤楼”,重檐三层,全用五色玻璃制成,太阳一照,光彩夺目;浙江的“镜湖亭”,中间嵌着一面直径2丈多的大圆镜,四壁用几万面小圆镜拼成鱼鳞模样,人在里面,一身可化作为亿万。
搭建一座华丽的楼阁,需要花去无数金银,官吏得到朝廷的嘉奖,人民却为此而遭了殃。
乾隆皇帝为了炫耀他的“圣绩”,大兴土木,广造官殿苑囿。
北京故宫的主要殿堂宫室,以及承德避暑山庄的主要建筑都是乾隆年间建造的。
北京的,虽始建于康熙四十二年,但在乾隆年间又作了大规模的改建和扩建。
圆明园是皇帝和、皇后的行宫之一,方圆30里,以水景为主,假山都用挖湖土堆成。
整个园林设计,既仿江南苏杭园林胜景和富家名园,又保留着北方园林风格。
还在长春园内仿意大利时期建西式楼阁群。
园内数以百计的宫殿楼阁、亭台、馆榭,除设着难以数计的艺术珍品,收藏着丰富的图书文物。
圆明园的建筑,汇集了全国各园精华,综合了中西艺术成就,是我国劳动人民智慧的结晶,也是建筑艺术的珍品。
可惜的是这个举世闻名的园林,在1860年英法联军侵入北京时,毁于一炬,建筑物全被烧光,金银财宝、古董珍奇被侵略者抢劫一空。
“千叟宴”的举行标志着乾隆盛世到了顶点,也是大清王朝开始衰落的起点。
从此它一天天地走向了衰落和崩溃。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
人教版七下数学知识点公式大全,初一党别错过!
2.对顶角:一个角的两边分别是另一个叫的两边的反向延长线,像这样的两个角互为对顶角。
3.垂线:两条直线相交成直角时,叫做互相垂直,其中一条叫做另一条的垂线。
4.平行线:在同一平面内,永不相交的两条直线叫做平行线。
5.同位角、内错角、同旁内角: 同位角:1与5、2与6像这样具有相同位置关系的一对角叫做同位角。
内错角:4与6、3与5像这样的一对角叫做内错角。
同旁内角:4与5、3与6像这样的一对角叫做同旁内角。
6.命题:判断一件事情的语句叫命题。
7.平移:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移变换,简称平移。
8.对应点:平移后得到的新图形中每一点,都是由原图形中的某一点移动后得到的,这样的两个点叫做对应点。
9.对顶角的性质:对顶角相等。
10.垂线的性质: 性质1:过一点有且只有一条直线与已知直线垂直。
性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
11.平行公理:经过直线外一点有且只有一条直线与已知直线平行。
平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
12.平行线的性质: 性质1:两直线平行,同位角相等。
性质2:两直线平行,内错角相等。
性质3:两直线平行,同旁内角互补。
13.平行线的判定: 判定1:同位角相等,两直线平行。
判定2:内错角相等,两直线平行。
判定3:同旁内角互补,两直线平行。
第六章 平面直角坐标系 一.知识框架 二.知识概念 1.有序数对:有顺序的两个数a与b组成的数对叫做有序数对,记做(a,b) 2.平面直角坐标系:在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系。
3.横轴、纵轴、原点:水平的数轴称为x轴或横轴;竖直的数轴称为y轴或纵轴;两坐标轴的交点为平面直角坐标系的原点。
4.坐标:对于平面内任一点P,过P分别向x轴,y轴作垂线,垂足分别在x轴,y轴上,对应的数a,b分别叫点P的横坐标和纵坐标。
5.象限:两条坐标轴把平面分成四个部分,右上部分叫第一象限,按逆时针方向一次叫第二象限、第三象限、第四象限。
注意:坐标轴上的点不在任何一个象限内。
第七章 三角形 一.知识框架 二.知识概念 1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2.三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边。
3.高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高。
4.中线:在三角形中,连接一个顶点和它的对边中点的线段叫做三角形的中线。
5.角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线。
6.三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性。
6.多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形。
7.多边形的内角:多边形相邻两边组成的角叫做它的内角。
8.多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角。
9.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
10.正多边形:在平面内,各个角都相等,各条边都相等的多边形叫做正多边形。
11.平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面。
12.公式与性质 三角形的内角和:三角形的内角和为180; 三角形外角的性质: 性质1:三角形的一个外角等于和它不相邻的两个内角的和。
性质2:三角形的一个外角大于任何一个和它不相邻的内角。
多边形内角和公式:n边形的内角和等于(n-2)·180 多边形的外角和:多边形的内角和为360。
多边形对角线的条数:从n边形的一个顶点出发可以引(n-3)条对角线,把多边形分词(n-2) 第八章 二元一次方程组 一.知识结构图 二、知识概念 1.二元一次方程:含有两个未知数,并且未知数的指数都是1,像这样的方程叫做二元一次。
方程,一般形式是 ax+by=c(a≠0,b≠0)。
2.二元一次方程组:把两个二元一次方程合在一起,就组成了一个二元一次方程组。
3.二元一次方程的解:一般地,使二元一次方程两边的值相等的未知数的值叫做二元一次方程组的解。
4.二元一次方程组的解:一般地,二元一次方程组的两个方程的公共解叫做二元一次方程组的解。
5.消元:将未知数的个数由多化少,逐一解决的想法,叫做消元思想。
6.代入消元:将一个未知数用含有另一个未知数的式子表示出来,再代入另一个方程,实现消元,进而求得这个二元一次方程组的解,这种方法叫做代入消元法,简称代入法。
7.加减消元法:当两个方程中同一未知数的系数相反或相等时,将两个方程的两边分别相加或相减,就能消去这个未知数,这种方法叫做加减消元法,简称加减法。
第九章 不等式与不等式组 一.知识框架 二、知识概念 1.用符号“<”“>”“ ”“”“≠”表示大小关系的式子叫做不等式。
2.不等式的解:使不等式成立的未知数的值,叫做不等式的解。
3.不等式的解集:一个含有未知数的不等式的所有解,组成这个不等式的解集。
4.一元一次不等式:不等式的左、右两边都是整式,只有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。
5.一元一次不等式组:一。
般地,关于同一未知数的几个一元一次不等式合在一起,就组成了一个一元一次不等式组 6.不等式的性质: 不等式的基本性质1:不等式的两边都加上(或减去)同一个数(或式子),不等号的方向不变。
不等式的基本性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
不等式的基本性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
第十章 数据的收集、整理与描述 一.知识框架 1.全面调查:考察全体对象的调查方式叫做全面调查。
2.抽样调查:调查部分数据,根据部分来估计总体的调查方式称为抽样调查。
3.总体:要考察的全体对象称为总体。
4.个体:组成总体的每一个考察对象称为个体。
5.样本:被抽取的所有个体组成一个样本。
6.样本容量:样本中个体的数目称为样本容量。
7.频数:一般地,我们称落在不同小组中的数据个数为该组的频数。
8.频率:频数与数据总数的比为频率。
9.组数和组距:在统计数据时,把数据按照一定的范围分成若干各组,分成组的个数称为组数,每一组两个端点的差叫做组距。
返回搜狐,查看更多
声明:本文内容仅代表作者个人观点,与本站立场无关。
如有内容侵犯您的合法权益,请及时与我们联系,我们将第一时间安排处理















